[ADv]

Вот в википедии.

Столбиком

Этот способ позволяет найти приближённое значение корня из любого действительного числа с любой наперёд заданной точностью.
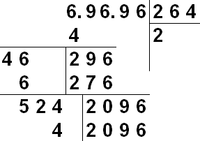
Для ручного извлечения корня применяется запись, похожая на деление столбиком. Пусть извлекается корень из целого числа A. В отличие от деления снос производится группами по 2 цифры, причём группы следует отмечать, начиная с десятичной запятой (в обе стороны), дописывая необходимым количеством нулей.

1. Найти an, квадрат которого наиболее близко подходит к группе старших разрядов числа A, оставаясь меньше последнего.
2. Провести вычитание из старших разрядов A квадрата числа an.
3. Удвоить an.
4. Сдвинуть остаток от вычитания на 2 разряда влево, а величину 2an — на один разряд влево. Под сдвигом в данном алгоритме понимается умножение/деление на степени 10, что соответственно является сдвигом влево и вправо.
5. Приписать справа от остатка вычитания два следующих старших разряда числа A.
6. Сравнить полученное число с нулём.
7. Если полученное число не равно 0, то найти такое 2an − 1, которое, будучи умноженным на , даст в результате число, меньшее полученного на четвёртом шаге, но наиболее близкое к нему по значению. Перейти к п.3.
8. Если в п.6 получено равенство, то перейти к п.4, предварительно приписав справа от an нуль.
9. После получения количества цифр, равного , прекратить вычисления (если требуется целое значение) или продолжать до необходимой точности, записывая получающиеся цифры после запятой.

Наглядное описание алгоритма:

Сообщение от Vivre

ну, мы же в школе это делали без калькуляторов! они, в мое время, еще не у всех были

Деление, умножение, вычитание и сложение мы действительно делали на бумажке, а вот корни, по крайней мере у нас, умели вычислять только самые продвинутые. А в старших классах и калькулятором разрешали пользоваться - там важнее было правильно интеграл взять, а не два числа перемножить.